一. 馬可夫模型(Markov Model)

以下會簡稱為MM。MM是一種具有狀態的隨機過程，從目前狀態轉移到下一個狀態 的機率由 P(下一個狀態|前一個狀態) 來決定(在 ‘前一個狀態’ 的前提下 ‘下一個狀態’ 發生的機率)，這些狀態的改變會變成一個穩態。上述的例子因為只看前一個狀態而已，故又稱為一階MM，可以以此類推至N階MM(在 ‘前N個狀態’ 的前提下 ‘下一個狀態’ 發生的機率)。

MM主要會有2個陣列組成:

• 狀態轉移陣列：當由一個狀態要轉移到下一個狀態時，會有相對應的轉移機率，這些機率會構成狀態轉移矩陣，通常假如有M個狀態會產生MxM的陣列，因此堂課主要是藉由昨天的天氣狀態與今天的天氣狀態為例，如下圖所示，此圖片為Coupy'NLP 100天馬拉松'裡的圖片。
  
• 初始機率陣列：也就是當前(最一開始)的狀態，如下圖，也就是說最一開始是晴天。
  

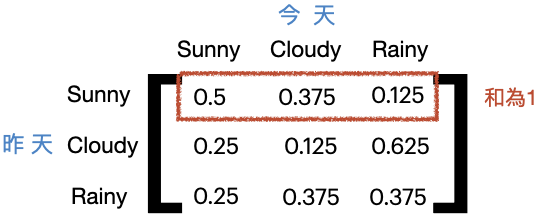
從上述可以了解，若今天天氣晴，隔天的各個天氣狀況會如下所示：
狀態轉移陣列的轉置 * 初始機率陣列，隔天天氣晴的機率為0.5，陰天的機率為0.375，雨天的機率為0.125:

二. 隱馬可夫模型(Hidden Markov Model)

以下皆簡稱為HMM，但在某些情況下，我們無法直接觀測到狀態資訊(ex：晴天、多雲、雨天)，就是所謂的隱態(HMM中，第一個字為何為Hidden的原因)，但我們可觀察其他的狀態來做推測，ex: 可以藉由觀察水草狀態(乾燥、濕潤、潮濕)來推測天氣的狀況。以NLP的POS來說，我們無法直接看出一個句字的中每個詞的詞性，所以詞性就是隱態，可以觀察到的狀態就是每個詞，也就是需要透過詞來推論詞性為何。

通常會比MM多一個陣列:

發射矩陣：隱藏狀態對應到每個觀察狀態的機率，以POS任務來說就是詞性(隱態)發生在每個詞的機率為何
用一個課堂上的例子: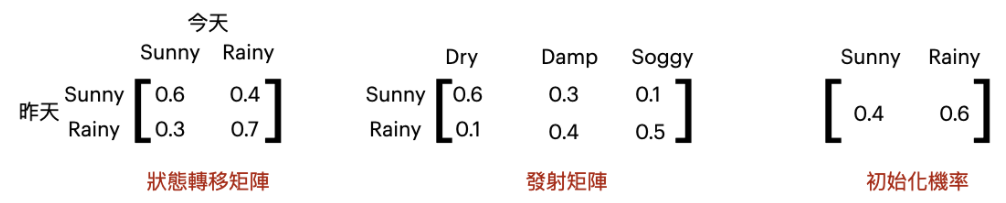

有上述這些陣列，若三天水草都是乾燥(Dry)，想推測這三天的天氣都是晴天的機率為多少，算法如下:

Sunny->Sunny->Sunny = (0.4 * 0.6) * (0.6 * 0.6) * (0.6 * 0.6) = 0.031104

1. 第一個 Sunny: Sunny 初始為 0.4，在 Dry 的狀態下是 Sunny 的機率 為 0.6 => 0.4*0.6

2. 第二個 Sunny：前一天是 Sunny 且今天也為 Sunny 的機率為 0.6，在Dry 的狀態下是 Sunny 的機率也是 0.6 => 0.6 * 0.6

3. 第三個 Sunny：前一天是 Sunny 且今天也為 Sunny 的機率為 0.6，在Dry 的狀態下是 Sunny 的機率也是 0.6 => 0.6 * 0.6

全部相乘即為所求

但這樣狂列出每個天氣情況的話會非常複雜，所有的機率都要個別算過一次才行知道哪種天氣組合的機率最大。現在我們來想一下若是POS問題的話，考慮一句話’我 很 帥’這個句子中每個詞的詞性，可以把詞性當成是graph的node，然後找出最有可能的詞性組合，就像下圖找到紅色箭頭這樣的路徑，‘我’對應到的詞性為’詞性1’，‘很’對應到的為’詞性2’，‘帥’對應到的為’詞性3’: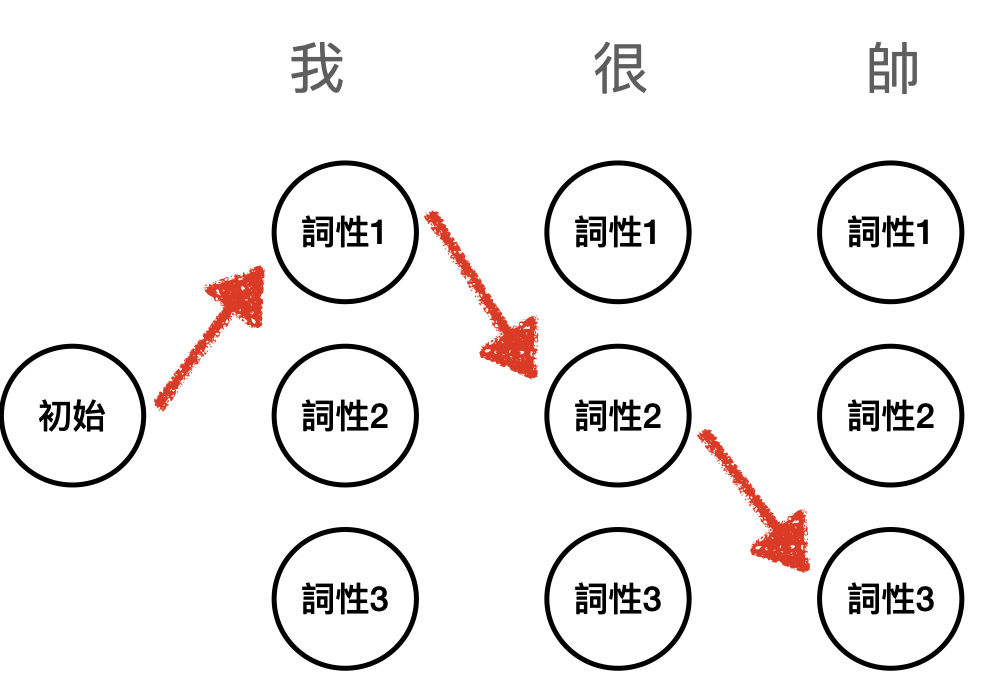

那要如何找到上面這條紅色的路徑，下一篇就會介紹一個Dynamic Programming的演算法: 為特比